在顺序结构以及平衡树中元素关键码与其存储位置之间没有对应的关系因此在查找一个元素时必须要经过关键码的多次比较。顺序查找时间复杂度为O(N)平衡树中为树的高度即O(logN)搜索的效率取决于搜索过程中元素的比较次数。

　　那么我们理想的搜索方法是可以不经过任何比较一次直接从表中得到要搜索的元素。

　　如果构造一种存储结构通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立一一映射的关系那么在查找时通过该函数可以很快找到该元素。

　　根据待插入元素的关键码以此函数计算出该元素的存储位置并按此位置进行存放

　　对元素的关键码进行同样的计算把求得的函数值当做元素的存储位置在结构中按此位置取元素比较若关键码相等则搜索成功

　　这种方式即为哈希(散列)方法哈希方法中使用的转换函数称为哈希(散列)函数构造出来的结构称为哈希表(Hash Table)(或者称散列表)

　　虽然上面的方法确实很快但是当新插入的元素为44时就会出现一个问题新的数据放哪

　　一般来说解决哈希冲突的方法有两种分别是闭散列与开散列

　　闭散列也叫开放定址法当发生哈希冲突时如果哈希表未被装满说明在哈希表中必然还有空位置那么可以把key存放到冲突位置中的“下一个” 空位置中去。那如何寻找下一个空位置呢

　　第一种是线c;即从发生冲突的位置开始依次向后探测直到寻找到下一个空位置为止。

　　现在需要插入元素44先通过哈希函数计算哈希地址为4因此44理论上应该插在该位置但是该位置已经放了值为4的元素即发生哈希冲突。

　　线a;一旦发生哈希冲突所有的冲突连在一起容易产生数据“堆积”即不同关键码占据了可利用的空位置使得寻找某关键码的位置需要许多次比较导致搜索效率降低。哈希游戏如何缓解呢

　　研究表明当表的长度为质数且表装载因子a不超过0.5时新的表项一定能够插入而且任何一个位置都不会被探查两次。因此只要表中有一半的空位置就不会存在表满的问题。在搜索时可以不考虑表装满的情况但在插入时必须确保表的装载因子a不超过0.5如果超出必须考虑增容。

　　因此我们可以知道闭散列最大的缺陷就是空间利用率比较低这也是哈希的缺陷。

　　开散列法又叫链地址法(开链法)首先对关键码集合用散列函数计算散列地址具有相同地址的关键码归于同一子集合每一个子集合称为一个桶各个桶中的元素通过一个单链表链接起来各链表的头结点存储在哈希表中。

　　从上图可以看出开散列中每个桶中放的都是发生哈希冲突的元素。

　　在存储效率上闭散列采用顺序表存储存储效率较高。而开散列采用单链表存储方式因为附加了指针域空间开销相对较大在冲突解决方式上闭散列方法是在哈希表中寻找下一个空闲位置来解决冲突因此容易产生堆积查找不易实现可能需要二次再查找。而开散列方法则是将冲突的关键码存储在另一个数据结构中避免了堆积现象查找相对容易。

　　综上所述闭散列和开散列在存储效率和冲突解决方式上存在差异具体选择哪种方案需要根据实际情况来决定。

　　给40亿个不重复的无符号整数没排过序。给一个无符号整数如何快速判断一个数是否在这40亿个数中。

　　数据是否在给定的整形数据中结果是在或者不在刚好是两种状态那么可以使用一个二进制比特位来代表数据是否存在的信息如果二进制比特位为1代表存在为0代表不存在。

　　布隆过滤器是由布隆Burton Howard Bloom在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构特点是高效地插入和查询可以用来告诉你 “某样东西一定不存在或者可能存在”它是用多个哈希函数将一个数据映射到位图结构中。此种方式不仅可以提升查询效率也可以节省大量的内存空间。

　　当向位图中插入一个数据时会先根据不同的哈希函数计算出不同的对应下标然后将对应的值标记成1再插入一个值时有

　　在查找时可以按照以下方式进行查找分别计算每个哈希值对应的比特位置存储的是否为零只要有一个为零代表该元素一定不在哈希表中否则可能在哈希表中。

　　注意布隆过滤器如果说某个元素不存在时该元素一定不存在如果该元素存在时该元素可能存在因为有些哈希函数存在一定的误判。举个例子如在布隆过滤器中查找某个元素是否存在时假设3个哈希函数计算的哈希值刚好和其他元素的比特位重叠此时布隆过滤器告诉该元素存在但实该元素是不存在的。

　　那么如何删除元素呢其实布隆过滤器不能直接支持删除工作因为在删除一个元素时可能会影响其他元素。举个例子在删除上图中apple元素时如果直接将该元素所对应的二进制比特位置0“banana”元素也被删除了因为这两个元素在多个哈希函数计算出的比特位上刚好有重叠。那我们该如何进行删除操作呢在此可以给出一种支持删除的方法将布隆过滤器中的每个比特位扩展成一个小的计数器插入元素时给k个计数器(k个哈希函数计算出的哈希地址)加一删除元素时给k个计数器减一通过多占用几倍存储空间的代价来增加删除操作。但是这种方法也有缺陷即存在计数回绕当计数器的值达到其最大值例如32位整数的最大值时再次增加计数器的值会导致其回到最小值0。这在布隆过滤器中可能会导致问题因为如果一个元素被删除了计数器减一然后再次入计数器加一那么这个元素的计数器可能会回绕到最初的0即使这个元素实际上仍然存在于布隆过滤器中。

　　1. 增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数一般比较小)与数据量大小无关

　　3. 布隆过滤器不需要存储元素本身在某些对保密要求比较严格的场合有很大优势

　　4. 在能够承受一定的误判时布隆过滤器比其他数据结构有这很大的空间优势

　　5. 数据量很大时布隆过滤器可以表示全集其他数据结构不能

　　在这里我们需要用到哈希切割在这之前我们要先了解一下什么是哈希切割

　　哈希切割是一种将大文件分割成多个小文件的方法其本质是将小文件当做哈希桶将大文件中的query通过哈希函数映射到这些哈希桶中如果是相同的query则会产生哈希冲突进入到同一个小文件中。

　　这样经过切分后不同的ip地址就存入了不同的小文件中此时再用map去统计各个小文件中ip出现次数即可

　　对此我们可以用两个位图来分别标识两个文件中的数据第一个文件遇见一个数就将第一个位图的对应位置set为1第二个文件遇见就将第二个位图的对应位置set为1在标识完所有数据后将两个位图&一下这样得到的位图中所有为1的数据即为交集

　　对此我们采取与第一个方式差不多的方法即用两个位图标识一个数标识完所有的数后找到所有为01或者10的数据即为出现次数不超过两次的整数。

　　对此我们可以用哈希切分来解决问题具体解决如下

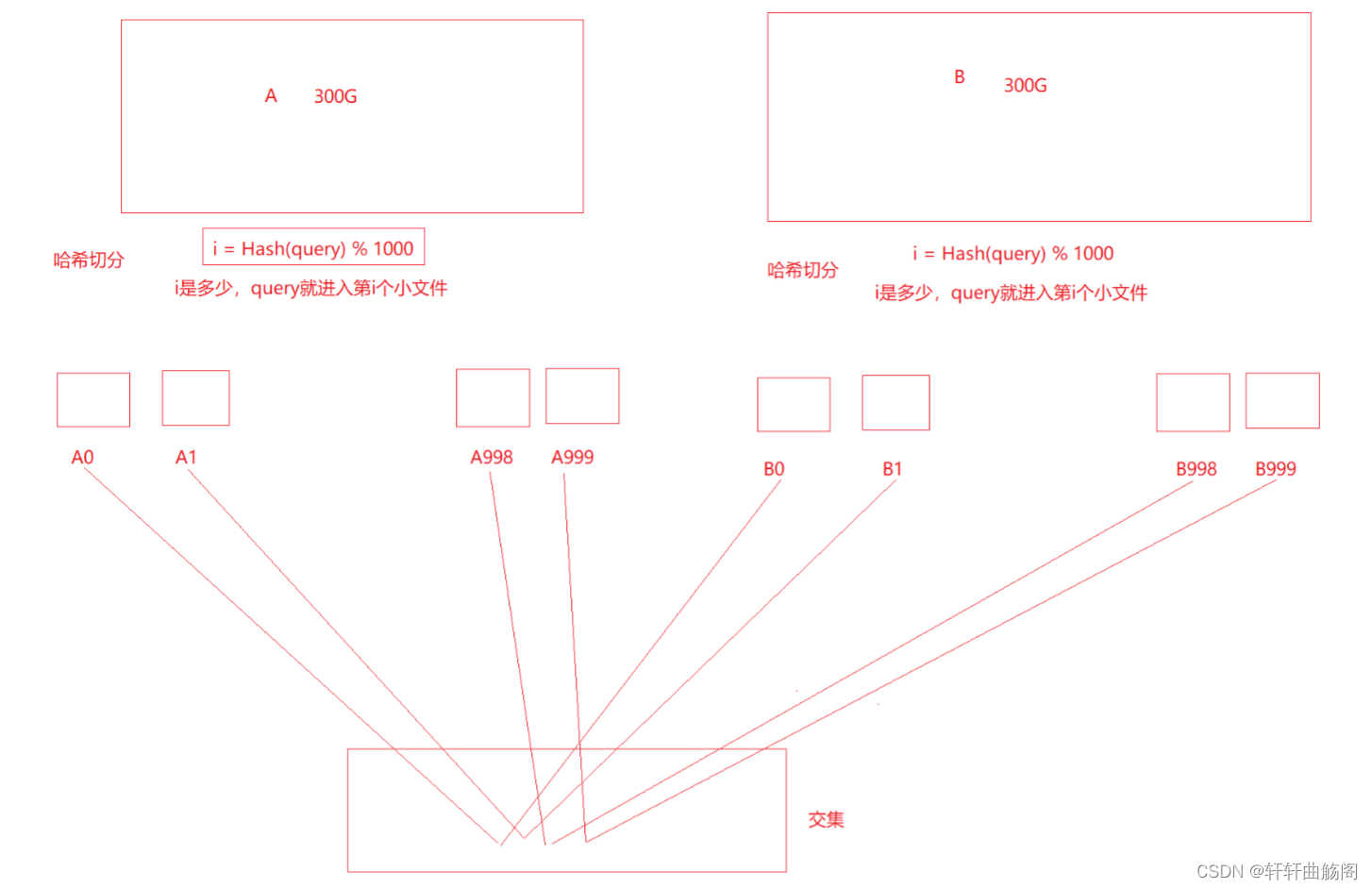
　　但是这种解决办法存在一些问题哈希切分并不是均匀的切分当哈希冲突过多时某一个文件会超出预计的1G内存此时又该如何解决呢

　　此时这个文件可以被分为两种情况一种是大部分query相同少部分相冲突另一种是大部分的query都是相冲突的。对此我们的解决方案如下

　　2.如果结果是抛异常的话需要更换一个哈希函数进行二次切分即将这个小文件进行再次的哈希切分。